
题目描述
993. 二叉树的堂兄弟节点
在二叉树中,根节点位于深度 0 处,每个深度为 k 的节点的子节点位于深度 k+1 处。
如果二叉树的两个节点深度相同,但 父节点不同 ,则它们是一对堂兄弟节点。
我们给出了具有唯一值的二叉树的根节点 root ,以及树中两个不同节点的值 x 和 y 。
只有与值 x 和 y 对应的节点是堂兄弟节点时,才返回 true 。否则,返回 false。
示例 1:
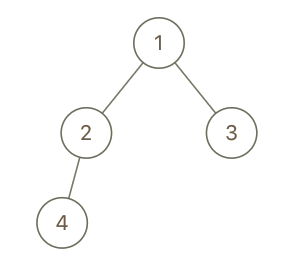
1
2
| 输入:root = [1,2,3,4], x = 4, y = 3
输出:false
|
示例 2:
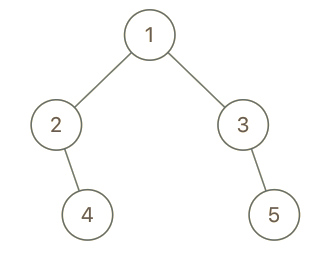
1
2
| 输入:root = [1,2,3,null,4,null,5], x = 5, y = 4
输出:true
|
示例 3:
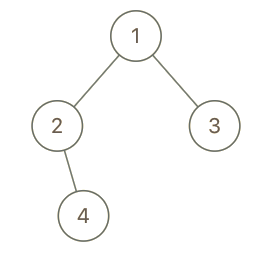
1
2
| 输入:root = [1,2,3,null,4], x = 2, y = 3
输出:false
|
提示:
- 二叉树的节点数介于
2 到 100 之间。
- 每个节点的值都是唯一的、范围为
1 到 100 的整数。
解题思路
通过两个节点的深度和父节点判断是否为堂兄弟节点。
遍历二叉树,分别记录两个节点的深度和父节点,若深度相同,父节点不同则为堂兄弟节点。
遍历可采用深度优先搜索或广度优先搜索。
代码实现
深度优先搜索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| public class Solution993Case2 {
static int xValue;
static int xDept;
static TreeNode xParent;
static boolean xFound;
static int yValue;
static int yDept;
static TreeNode yParent;
static boolean yFound;
public static boolean isCousins(TreeNode root, int x, int y) {
xValue = x;
yValue = y;
dfs(root, 0, null);
return xDept == yDept && xParent != yParent;
}
private static void dfs(TreeNode node, int dept, TreeNode parent) {
if (node == null) {
return;
}
if (node.val == xValue) {
xDept = dept;
xParent = parent;
xFound = true;
}
if (node.val == yValue) {
yDept = dept;
yParent = parent;
yFound = true;
}
if (xFound && yFound) {
return;
}
dfs(node.left, dept + 1, node);
if (xFound && yFound) {
return;
}
dfs(node.right, dept + 1, node);
}
public static void main(String[] args) {
TreeNode node4 = new TreeNode(4);
TreeNode node5 = new TreeNode(5);
TreeNode node2 = new TreeNode(2, null, node4);
TreeNode node3 = new TreeNode(3, null, node5);
TreeNode node1 = new TreeNode(1, node2, node3);
System.err.println(isCousins(node1, 5, 4));
}
}
|



