每日一题-20240119

发表于 更新于 分类于 阅读次数： 本文字数： 393 阅读时长 ≈ 1 分钟

题目描述

2319. 判断矩阵是否是一个 X 矩阵

如果一个正方形矩阵满足下述 全部 条件，则称之为一个 X 矩阵 ：

  1. 矩阵对角线上的所有元素都 不是 0
  2. 矩阵中所有其他元素都是 0

给你一个大小为 n x n 的二维整数数组 grid ，表示一个正方形矩阵。如果 grid 是一个 X 矩阵 ，返回 true ；否则，返回 false 。

示例 1：

img

1
2
3
4
5
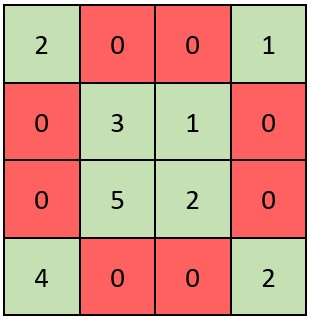
输入：grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
输出：true
解释：矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 是一个 X 矩阵。

示例 2：

img

1
2
3
4
5
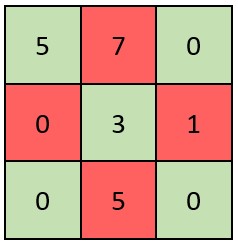
输入：grid = [[5,7,0],[0,3,1],[0,5,0]]
输出：false
解释：矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 不是一个 X 矩阵。

提示：

  • n == grid.length == grid[i].length
  • 3 <= n <= 100
  • 0 <= grid[i][j] <= 105

解题思路

观察法，观察对角线上的数有哪些规律。

假设一个n×n的二维整数数组 grid[i][j]，则以下为对角线上的数：

  1. i=j
  2. i + j + 1 = n

代码实现

源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class Solution2319 {
    public static boolean checkXMatrix(int[][] grid) {
        for (int i = 0; i < grid.length; i++) {
            for (int j = grid.length - 1; j >= 0; j--) {
                if (i == j) {
                    if (grid[i][j] == 0) {
                        return false;
                    }
                } else {
                    if (j == grid.length - 1 - i) {
                        if (grid[i][j] == 0) {
                            return false;
                        }
                    } else if (grid[i][j] != 0) {
                        return false;
                    }
                }
            }
        }
        return true;
    }

    public static void main(String[] args) {
        int[][] grid = {{2, 0, 0, 1}, {0, 3, 1, 0}, {0, 5, 2, 0}, {4, 0, 0, 2}};
        System.err.println(checkXMatrix(grid));
    }
}